Co-Design or the Best of Both Worlds

This is still a work in progress blog post. The deadline for this project is set to Monday 9th of December. Moreover, I may need some time to clean up the git repo and make it available at the time of this publication.

Abstract

In this blogpost, we explore the multiple design steps we went through to design a Co-Design implementation of the RSA algorithm using the Pynq Z-2 and C code combined with ARM assembly. We will motivate our design choices and provide some insights and metrics about the implementation. Finally, we will explain how we tested our implementation and benchmarked it.

The RSA algorithm

The RSA algorithm is at the core of many telecommunications systems and is extensively use. Asymetric key encryption is pretty straight forward on paper but implementing it in Hardware is not as easy as one may think.

In this project, we explored how we can design faster modulo multiplication by using the Montgomery representation which really comes handy in Hardware.

After building this Montgomery multiplier, we used a bit of C code to interface with the FPGA board and running the power ladder in software but deallocating the power hungry modulo multiplication to the board.

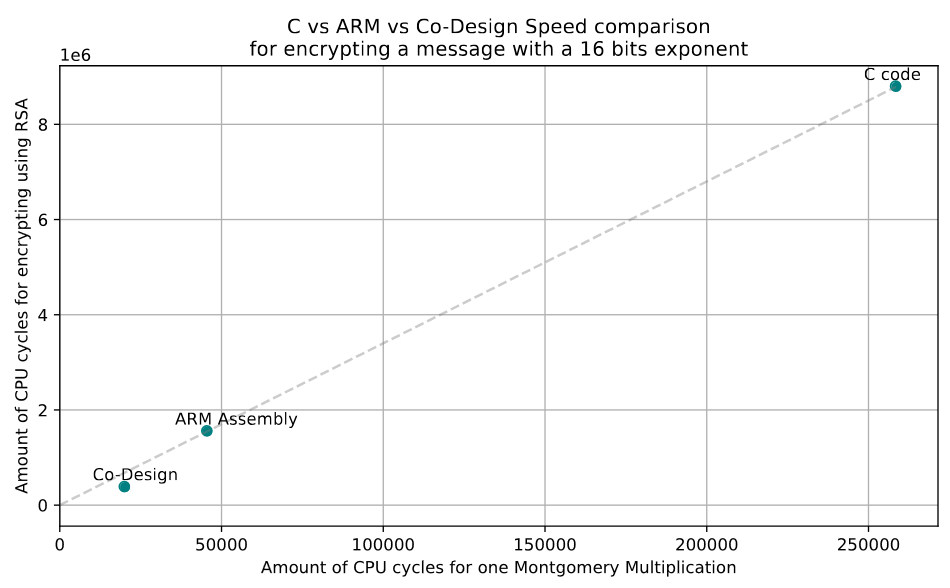
Here is a little sneak peek of our results.

Going Beyond

We also push the project a bit further by implementing a small library of functions to make this project useful on a daily basis. We added the possibility to encrypt actual string of texts.

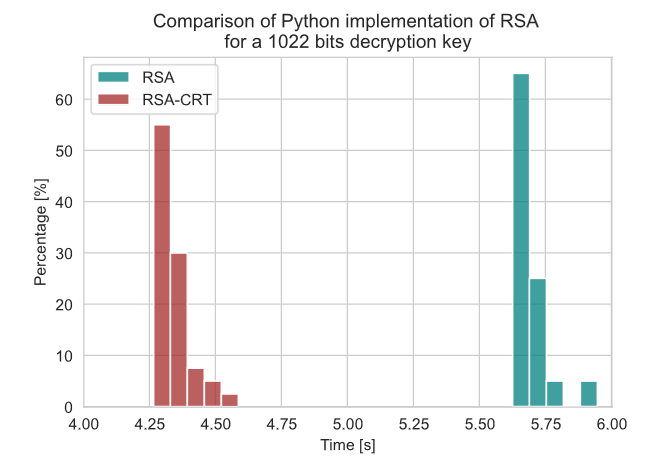
Making it convenient is one thing but making it faster is even better ! This is what motivates me and pushed me to dig some ancient Chinese math. On a more serious note, many RSA implementation use the Chinese Remainder Theorem.

The most expensive part of the algorithm is the decryption and the asymmetric encryption/decryption power consumption is a major flaw in RSA. For instance, we mostly encrypt using 16 bits key, but so most decryption can use up to 1024 bits key ! That’s why the Chinese Remainder Theorem is so useful as it speeds up the process by roughly 40%. But keep in mind the extra amount of informations that need to be transmitted to let the receiver use this technique.

This is the algorithm for decrypting a message using the CRT and we measured some significant speed up. Here is another figure from the paper. If you are curious to learn more about it I highly suggest you to read the paper ;).

The paper

You can download the full PDF by clicking here :