This blog post is still a work in progress
In this project for my DSP class, we used matlab (huhhhh take me back to python and scipy) for running some lab experiments about transmitting pictures through the acoustic channel. In other words, we learn how to make loud noises that sound horrible but somehow gives pretty pictures
Matlab
This project was using matlab and my goodness it is huhhh. While it is a wonderful piece of software that makes development and translation from math to code really more trivial, I can help but hate that added level of abstractions. To be fair, my opinion is totally biased since I come from the Software world so python has been my goto for the past 5 years.
In Matlab, there is a function for everything which is a blessing and a curse. While it made some bits of this project more simple since we didn’t have to reinvent the wheel, it also added some abstraction and less flexibility and we had to be a bit more creative.
Simulink, on the other hand is a treasure, I really envy this to Matlab and I think the python community should develop a similar tool which would be the absolute Matlab killer.
The project
Enough rant about my love-hate relationship with a piece of code. The project was about using OFDM on QAM symbol to send data through the air which is heavily used in Wi-Fi (with beamforming, optimization algorithm, Reed-Solomon, … but it is not the main subject of this course). The idea behind Orthogonal Frequency Division Multiplexing is quite simple and ingenious, we use various symbol that won’t interfere with each other.
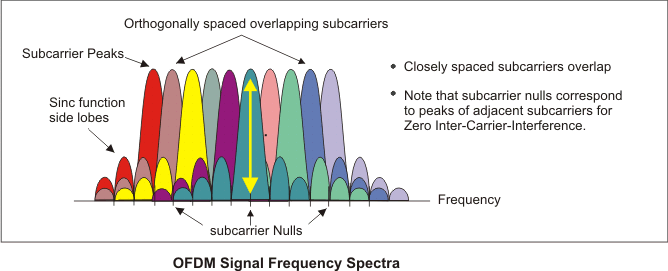
We have multiple subcarrier that are designed in a way that the peak of one is located at the lobe of all of the others avoiding some interferences.
The cherry on top is the use of QAM symbol which are complex value symbols and so previously, we had to rely on sending $cos$ and $sin$ wave to mimick the quadrature and in phase parts. Which is prone to error, to frequency shift, … Modulating those QAM Symbols by using OFDM and some clever math makes each symbol a sort of raised cosine.
From complex to sound
As you all know, sending complexe value symbol is not really a thing so we can only rely on sending real valued data so the speaker can reproduce it and transmit the data. But how to come from a QAM to a real value symbol ? DFT and some symmetry !
To run this we need to setup our dataframe in such ways that every symbols $S$ is set as :
\[\begin{bmatrix} 0\\ S_1\\ S_2\\ \vdots\\ S_N\\ 0\\ S_N^*\\ \vdots\\ S_2^*\\ S_1^* \end{bmatrix}\]Which, if you multiply with a DFT matrix, will give you a real valued signals by canceling all complex parts of this vector. Of course, this can be generalized for multiple frame in parallel and then realize a parallel to serial conversion (np.reshape()) to transform a matrix into a vector. And that’s it ! The OFDM is “simply” a DFT over a specific set of QAM Symbols. It’s so simple you wouldn’t believe it.
Noise & Channel
One of the main concern here is the issue with noise but we can’t do much about it. The bigger issue here is the channel and how some frequency (i.e. OFDM Symbol) may be more prone to error since they are not “well transmitted” through the channel. So we need to compensate for it.
Evaluation of the channel
First, it gives some idea of how each frequency (i.e. OFDM frames) are affected by the frequency of the channel and we can compute an approximation of the inverse of the channel to try to compensate for the losses. One simple to have a channel estimate is by sending multiple training frames and averaging them out or using some minimizing technique to make sure the Gaussian Noise has as little impact as possible.